
We bring you a brand new Mensa Cats cartoon by J.B. (that’s Jason Berry of Vacuum Tree Head). This one expresses not one but two of Zeno’s famous paradoxes in a single frame.
The first is the better-known Dichotomy Paradox, from which the punchline derives. In order to walk into the bar, Zeno (or any of the other patrons) must first walk halfway; and to travel from the halfway point, he must travel half of that distance, and then half of that distance, and so on. It seems that this process of walking halfway would continue forever and one would not arrive and one’s destination, yet we know in reality that we do.
The second paradox is the Arrow Paradox. Consider the frame frozen in time, as indicated by the liquid in mid spill behind the young lady cat, or the multiple instances of Zeno along his path. At any given moment, there is no motion. Zeno’s position does change between moment, but there is an infinite number of other frames, each with a fixed position. As copies/frames of Zeno get closer and closer together, the change in time between them gets infinitesimally small. Yet the process 0f adding up these infinite frames with zero motion in each results in Zeno walking halfway into the bar.
The two paradoxes (and the third, commonly referred to as “Achilles and the tortoise”) are closely related. The first deals with infinitesimal subdivisions of space, while the second deals with infinitesimal subdivisions of time. The key is that while any infinitesimal quantity is smaller than any quantity we can express, it is always still greater than zero. And adding up an infinite number of infinitesimal quantities can sometimes yield a finite number.
Take the halving process in the Dichotomy paradox. Zeno moves half this distance, then half of that, and so on. This can be expressed as an infinite sum.
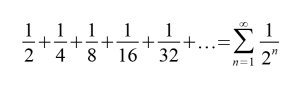
As one gets closer to infinity, the sum gets closer and closer to one. More formally, we can say that as we approach infinity, the sum goes to 1. So an infinite number of subdivisions still reaches our goal of the full distance.
This process of applying operations to an infinite number of infinitesimal subdivisions is the principal behind calculus, and a marvelous thing to behold once one gets used to it. The mathematics does not necessarily answer the metaphysical questions raised by these ancient paradoxes, but it is what most interests us at CatSynth. It’s been a while since we last shared the joy and beauty of mathematics on these pages, but it is high time we resume the practice.

I love thinking about this kind of thing. Reminds me of the “Coastline Paradox” http://www.maproomblog.com/2018/03/the-coastline-paradox/ Infinity is weird stuff.
The Coastline Paradox as a great one, too! Again, mathematics provides a way out of the paradox without necessarily resolving the philosophical questions. 😺